A polynomial p(x) is the expression in variable x which is in the form (axn + bxn-1 + …. + jx+ k), where a, b, c …., k fall in the category of real numbers and 'n' is non negative integer, which is called the degree of polynomial.

An essential characteristic of the polynomial is that each term in the polynomial expression consists of two parts:

• Coefficient
• Exponent

Example :

10x² + 26x, here 10 and 26 are coefficients and 2, 1 is its exponential value.

Points to keep in Mind while working with Polynomials :

• The sign of each coefficient and exponent is stored within the coefficient and the exponent itself.
• Additional terms having equal exponent is possible one.
• The storage allocation for each term in the polynomial must be done in ascending and descending order of their exponent.

Representation of polynomial :

Polynomial can be represented in the various ways. These are:

• Using array
• Using linked list

Polynomial using linked list:

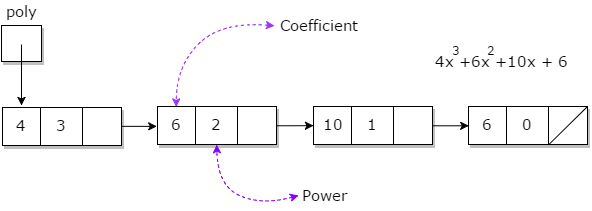
We store each polynomial as a singly linked list where each node stores the exponent and coefficient in the data part and a reference to the next node as shown in the figure below. Their sum is then stored in another linked list

Procedure :

We store each polynomial as a singly linked list where each node stores the exponent and coefficient in the data part and a reference to the next node as shown in the figure below. Their sum is then stored in another linked list

Algorithm

Step 1: Start.
Step 2: Define user defined datatype node consisting of int coefficient and exponent and a pointer next of type node.
Step 3: Defining create function
	struct node* create(struct node* head, int co, int exp)
		Check if(head == Null)
			temp <- GetNode(node)
			temp.co <- co
			temp.exp <- exp
			temp.next <- Null
			Set head <- temp
		otherwise
			Set temp <- head
			while(temp.next ≠ Null) do
				temp <- temp.next
			flag <- GetNode(node)
			flag.co <- co
			flag.exp <- exp
			flag.next <- Null
			temp.next <- flag
	         return head

Step 4: Defining Addition function
	struct node* polyAdd(struct node *p1, struct node *p2, struct node *sum)
		Set poly1 <- p1
		Set poly2 <- p2
		Set result <- Null
		check if(poly1 ≠ Null AND poly2 == Null) 
			Set sum <- poly1
			Return sum
		else if(poly1 == Null AND poly2 ≠ Null)
			Set sum <- poly2
			Return sum
		while(poly1 ≠ Null AND poly2 ≠ Null) do
			Check if(sum == Null)
				sum <- GetNode(node)
				Set result  <- sum
			Otherwise
				result.next <- GetNode(node)
				Set result <- result.next
			Check if(poly1.exp > poly2.exp)
				Set result.co <- poly1.co
				Set result.exp <- poly1.exp
				Set poly1 <- poly1.next
			Check if(poly1.exp < poly2.exp)
				Set result.co <- poly2.co
				Set result.exp <- poly2.exp
				Set poly2 <- poly2.next
			Otherwise
				Set result.co <- poly1.co + poly2.co
				Set result.exp  <- poly1.exp
				Set poly1  <- poly1.next
				Set poly2  <- poly2.next
		while(poly1 ≠ Null) do
			Set result.next  <- GetNode(node)
			Set result <- result.next
			Set result.co <- poly1.co
			Set result.exp <- poly1.exp
			Set poly1 <- poly1.next
		while(poly2 ≠ Null) do
			Set result.next <- GetNode(node)
			Set result  <- result.next
			Set result.co <- poly2.co
			Set result.exp <- poly2.exp
			Set poly2 <- poly2.next
		Set result.next <- Null
		Return sum

Step 5: Defining Display function
	void display(struct node* head)
		Set temp <- head
		while(temp ≠ Null) do
			Display temp.co, temp.exp
			Set temp <- temp.next

Step 6: Defining Main function
	Set p1 <- Null
	Set p2 <- Null
	Set sum <- Null
	Set flag <- 1
	while(flag == 1) do
		Display “1: Create Polynomial 1”
		Display “2: Create Polynomial 2”
		Display “3: Perform Addition”
		Display “4: Exit”
		Read choice
		switch(choice)
			Case 1:
				Display “Enter coefficient for polynomial 1”
				Read co
				Display “Enter exponent for polynomial 1”
				Read exp
				Call create(p1, co, exp)
			Case 2: 
				Display “Enter coefficient for polynomial 2”
				Read co
				Display “Enter exponent for polynomial 2”
				Read exp
				Call create(p2, co, exp)
			Case 3:
				Set sum <- call polyAdd(p1, p2, sum)
				Call display(sum)
			Case 4:
				Set flag <- 0
		End switch

Step 7: Stop

Program using C

//CIRCULAR SINGLY LINKED LIST #include <stdio.h> #include <stdlib.h> //polynomial node structure struct node struct node { int co, exp; struct node* next; }; //create a polynomial struct node* create (struct node* head, int co, int exp) { struct node *temp, *flag; //if polynomial empty. make the node the head node if(head == NULL) { temp = (struct node*)malloc(sizeof(struct node)); temp->co = co; temp->exp = exp; temp->next = NULL; head=temp; } else { //else go to the last node and append temp = head; while(temp->next != NULL) temp = temp->next; flag = (struct node *)malloc(sizeof(struct node)); flag->co = co; flag->exp = exp; flag->next = NULL; temp->next = flag; } return head; } //add two polynomial struct node* polyAdd (struct node *p1, struct node *p2, struct node *sum) { //copy the two polynomial and initialize variable res to store the sum struct node *poly1 = p1, *poly2 = p2, *res; //if polynomial 2 is null, set polynomial 1 as the sum if(poly1 != NULL && poly2 == NULL) { sum = poly1; return sum; } //if polynomial 1 is null, set polynomial 2 as the sum else if(poly1 == NULL && poly2 != NULL) { sum = poly2; return sum; } //if both polynomials are non-empty while (poly1 != NULL && poly2 != NULL) { //if the sum is empty, initialize sum with a node structure //and set res equal to sum if(sum == NULL) { sum = (struct node *)malloc(sizeof(struct node)); res = sum; } //add a new node structure at the end of res to store sum else { res->next = (struct node *)malloc(sizeof(struct node));; res = res->next; } //if exponent of current node of polynomial 1 is greater than that of polynomial 2 //add it to the sum if (poly1->exp > poly2->exp) { res->co = poly1->co; res->exp = poly1->exp; poly1 = poly1->next; } //if exponent of current node of polynomial 2 is greater than that of polynomial 1 //add it to the sum else if (poly1->exp < poly2->exp) { res->co = poly2->co; res->exp = poly2->exp; poly2 = poly2->next; } //if exponent of current node of polynomial 1 is equal to that of polynomial 2 //add the sum of their co-efficient to the sum else if(poly1->exp == poly2->exp) { res->co = poly1->co + poly2->co; res->exp = poly1->exp; poly1 = poly1->next; poly2 = poly2->next; } } //if polynomial 1 is non-empty add the remaining nodes to the sum while (poly1 != NULL) { res->next = (struct node *)malloc(sizeof(struct node));; res = res->next; res->co = poly1->co; res->exp= poly1->exp; poly1 = poly1->next; } //if polynomial 2 is non-empty add the remaining nodes to the sum while (poly2 != NULL) { res->next = (struct node *)malloc(sizeof(struct node));; res = res->next; res->co = poly2->co; res->exp = poly2->exp; poly2 = poly2->next; } //set pointer of last node to null res->next = NULL; //return the head node of the sum return sum; } //display polynomial void display (struct node* head) { struct node *temp=head; while (temp != NULL) { printf("%d^%d+",temp->co,temp->exp); temp=temp->next; } printf("\n"); } void main() { //to store polynomial 1, polynomial 2 and the sum struct node *p1 = NULL, *p2 = NULL, *sum = NULL; int ch, co, exp; int loop= 1; while(loop) { printf("1. Add to Polynomial 1\n"); printf("2. Add to Polynomial 2\n"); printf("3. Perform Addition\n"); printf("4. Exit\n"); scanf("%d", &ch); switch(ch) { case 1: printf("Enter co-efficient\n"); scanf("%d", &co); printf("Enter exponent\n"); scanf("%d", &exp); p1 = create(p1, co, exp); break; case 2: printf("Enter co-efficient\n"); scanf("%d", &co); printf("Enter exponent\n"); scanf("%d", &exp); p2 = create(p2, co, exp); break; case 3: sum=polyAdd (p1, p2, sum); printf("\nPolynomial 1\n"); display(p1); printf("\nPolynomial 2\n"); display(p2); printf("\nSum: \n"); display (sum); break; case 4: loop = 0; break; default: printf("Wrong Choice! Re-enter\n"); break; } } }