Merge Sort

Merge Sort is one of the most popular sorting algorithms that is based on the principle of Divide and Conquer Algorithm.

Here, a problem is divided into multiple sub-problems. Each sub-problem is solved individually. Finally, sub-problems are combined to form the final solution.

Divide and Conquer Strategy :

Using the Divide and Conquer technique, we divide a problem into sub-problems. When the solution to each subproblem is ready, we 'combine' the results from the sub-problems to solve the main problem.

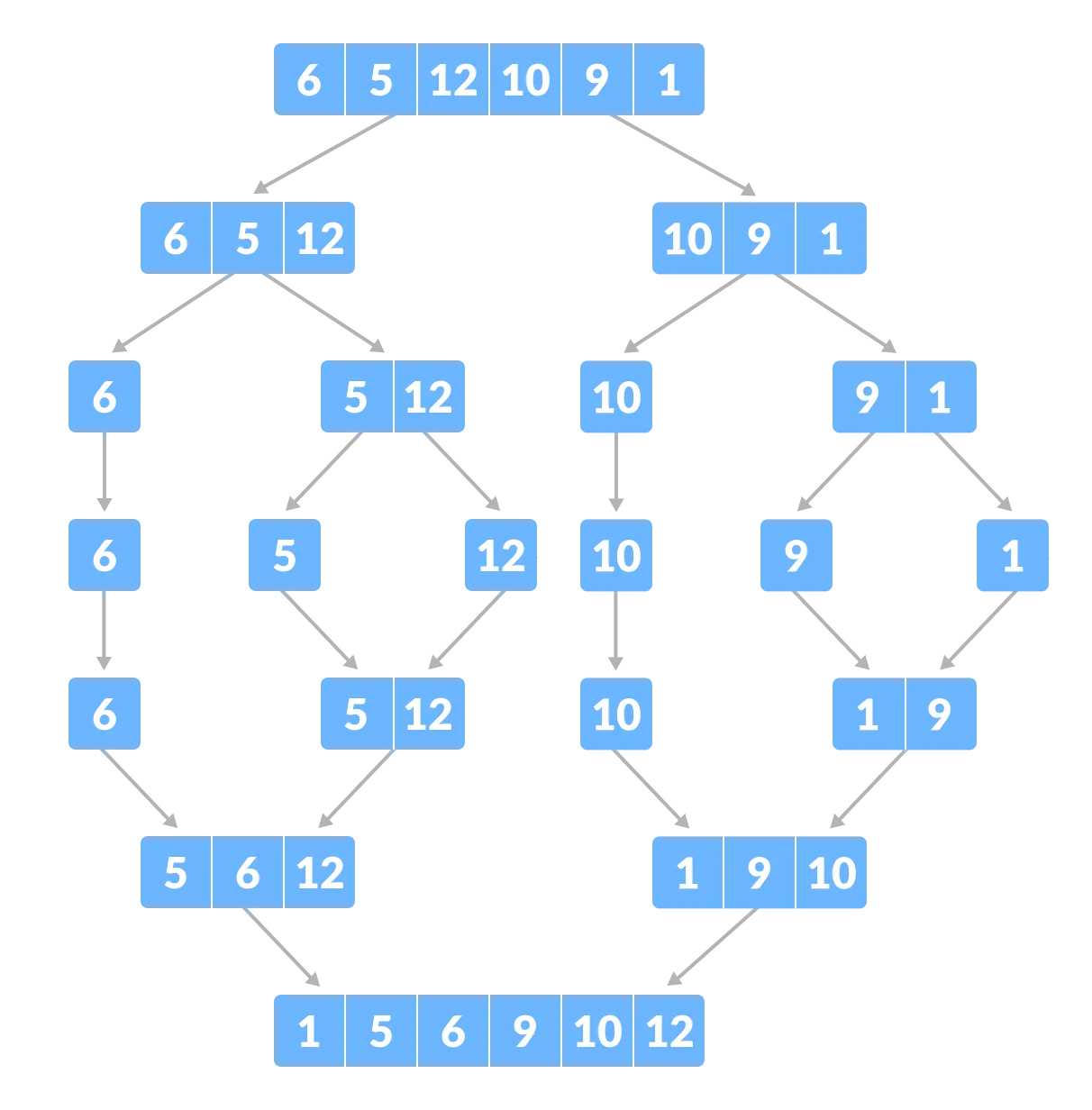
Suppose we had to sort an array A. A subproblem would be to sort a sub-section of this array starting at index p and ending at index r, denoted as A[p..r].

Divide

If q is the half-way point between p and r, then we can split the subarray A[p..r] into two arrays A[p..q] and A[q+1, r].

Conquer

In the conquer step, we try to sort both the sub-arrays A[p..q] and A[q+1, r]. If we haven't yet reached the base case, we again divide both these sub-arrays and try to sort them.

Combine

When the conquer step reaches the base step and we get two sorted sub-arrays A[p..q] and A[q+1, r] for array A[p..r], we combine the results by creating a sorted array A[p..r] from two sorted sub-arrays A[p..q] and A[q+1, r]

Algorithm

In the following algorithm, arr is the given array, beg is the starting element, and end is the last element of the array.

                MERGE_SORT(arr, beg, end)  
                
                if beg < end  
                set mid = (beg + end)/2  
                MERGE_SORT(arr, beg, mid)  
                MERGE_SORT(arr, mid + 1, end)  
                MERGE (arr, beg, mid, end)  
                end of if  
                
                END MERGE_SORT

The important part of the merge sort is the MERGE function. This function performs the merging of two sorted sub-arrays that are A[beg…mid] and A[mid+1…end], to build one sorted array A[beg…end]. So, the inputs of the MERGE function are A[], beg, mid, and end.

Program using C

//MERGE SORT
#include <stdio.h>  
  
    /* Function to merge the sub-arrays of a[] */  
    void merge(int a[], int beg, int mid, int end)    
    {    
        int i, j, k;  
        int n1 = mid - beg + 1;    
        int n2 = end - mid;    
          
        int LeftArray[n1], RightArray[n2]; //temporary arrays  
          
        /* copy data to temp arrays */  
        for (int i = 0; i < n1; i++)    
        LeftArray[i] = a[beg + i];    
        for (int j = 0; j < n2; j++)    
        RightArray[j] = a[mid + 1 + j];    
          
        i = 0; /* initial index of first sub-array */  
        j = 0; /* initial index of second sub-array */   
        k = beg;  /* initial index of merged sub-array */  
          
        while (i < n1 && j < n2)    
        {    
            if(LeftArray[i] <= RightArray[j])    
            {    
                a[k] = LeftArray[i];    
                i++;    
            }    
            else    
            {    
                a[k] = RightArray[j];    
                j++;    
            }    
            k++;    
        }    
        while (i<n1)    
        {    
            a[k] = LeftArray[i];    
            i++;    
            k++;    
        }    
          
        while (j<n2)    
        {    
            a[k] = RightArray[j];    
            j++;    
            k++;    
        }    
    }    
      
    void mergeSort(int a[], int beg, int end)  
    {  
        if (beg < end)   
        {  
            int mid = (beg + end) / 2;  
            mergeSort(a, beg, mid);  
            mergeSort(a, mid + 1, end);  
            merge(a, beg, mid, end);  
        }  
    }  
      
    /* Function to print the array */  
    void printArray(int a[], int n)  
    {  
        int i;  
        for (i = 0; i < n; i++)  
            printf("%d ", a[i]);  
        printf("\n");  
    }  
      
    int main()  
    {  
        int a[] = { 12, 31, 25, 8, 32, 17, 40, 42 };  
        int n = sizeof(a) / sizeof(a[0]);  
        printf("Before sorting array elements are - \n");  
        printArray(a, n);  
        mergeSort(a, 0, n - 1);  
        printf("After sorting array elements are - \n");  
        printArray(a, n);  
        return 0;  
    }